Possible Bipartition

Medium Graph DFS BFS

Amazon

Facebook

eBay

2020-05-27

886. Possible Bipartition

Question:

Given a set of N people (numbered 1, 2, ..., N), we would like to split everyone into two groups of any size.

Each person may dislike some other people, and they should not go into the same group.

Formally, if dislikes[i] = [a, b], it means it is not allowed to put the people numbered a and b into the same group.

Return true if and only if it is possible to split everyone into two groups in this way.

Example 1:

Input: N = 4, dislikes = [[1,2],[1,3],[2,4]]
Output: true
Explanation: group1 [1,4], group2 [2,3]

Example 2:

Input: N = 3, dislikes = [[1,2],[1,3],[2,3]]
Output: false

Example 3:

Input: N = 5, dislikes = [[1,2],[2,3],[3,4],[4,5],[1,5]]
Output: false

Note:

1 <= N <= 2000
0 <= dislikes.length <= 10000
1 <= dislikes[i][j] <= N
dislikes[i][0] < dislikes[i][1]
There does not exist i != j for which dislikes[i] == dislikes[j].

Solution:

Similar to LeetCode Question 785, color each node with a color. The neighbours node should have a different color than yours. Then using BFS or DFS to check or assign the color to the node next to it.

The following picture demo borrowed from Huahua.

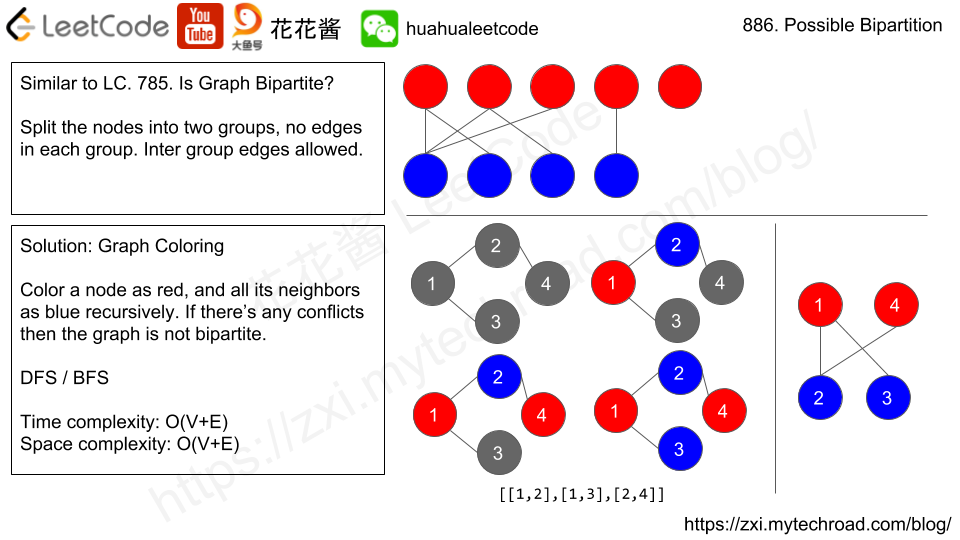
Using BFS:

class Solution {
    public boolean possibleBipartition(int N, int[][] dislikes) {
        if (dislikes == null || dislikes.length == 0) return true;
        HashMap<Integer, Set<Integer>> map = new HashMap<>();
        for (int[] i : dislikes) {
            int a = i[0];
            int b = i[1];
            map.putIfAbsent(a, new HashSet<Integer>());
            map.putIfAbsent(b, new HashSet<Integer>());
            map.get(a).add(b);
            map.get(b).add(a);
        }
        
        Queue<Integer> que = new LinkedList<>();
        int[] colors = new int[N + 1];
        
        for (int i = 1; i <= N; i++) {
            if (colors[i] != 0) continue;
            
            colors[i] = 1;
            que.offer(i);
            
            while (!que.isEmpty()) {
                int index = que.poll();
                if (!map.containsKey(index)) continue;
                for (int next: map.get(index)){
                    if (colors[next] == colors[index]) {
                        return false;
                    } 
                    if(colors[next] == 0) {
                        colors[next] = -colors[index];
                        que.offer(next);
                    }
                }
            }
        }
        return true;
    }
}

Using DFS:

class Solution {
    
    public int[] colors;
    public HashMap<Integer, Set<Integer>> map;
    
    public boolean possibleBipartition(int N, int[][] dislikes) {
        if (dislikes == null || dislikes.length == 0) return true;
        map = new HashMap<>();
        for (int[] i : dislikes) {
            int a = i[0];
            int b = i[1];
            map.putIfAbsent(a, new HashSet<Integer>());
            map.putIfAbsent(b, new HashSet<Integer>());
            map.get(a).add(b);
            map.get(b).add(a);
        }
        
        colors = new int[N + 1];
        for (int i = 1; i <= N; i++) {
            if (colors[i] == 0 && !dfs(i, 1)) return false;
        }
        return true;
    }
    
    private boolean dfs(int i, int targetcolor) {
        if (colors[i] != 0) return colors[i] == targetcolor;
        
        colors[i] = targetcolor;
        
        if (map.get(i) == null) return true;
        
        for (int next : map.get(i)) {
            if (!dfs(next, -targetcolor)) return false;
        }
        
        return true;
    }
}

Time complexity: O(V+E)
Space complexity: O(V+E)